統計学で扱う母集団は、その分布が正規分布であることを前提としています。下のグラフを見てみましょう。

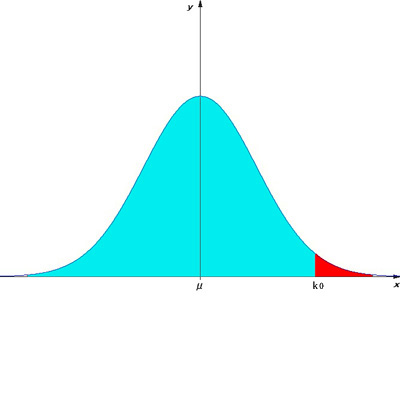
この図でμは母平均をあらわしています。

仮にこのグラフが全国の共通試験の分布を表しているとします。全国平均はμです。あるクラスの平均点は sであったとします。このとき、このクラスは全国平均と比べて優れているといえるかどうかを統計的に考えたいとき、まずある点数 k₀ を決めるとします。k₀ よりこのクラスの平均点 s が大きければ優れていると認めることにすればいいわけです。では k₀ はどのように設定すればいいのでしょうか？

統計学で多く使われているのが

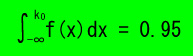
となる値 k₀ を定めることです。上位5%に入っていれば優れていると認めるわけです。つまり上のグラフでいうと、水色の部分の面積が0.95（全体の95%）になるように k₀ を決めます。（赤い部分は逆に0.05になるわけですが、この値のことを有意水準（危険率）といいます。）

しかし、いちいち95%になる値を計算するのではなく便利な標準正規分布表というものを用います。

正規分布は平均と分散のみでその密度関数N(μ,σ²)をあらわすことができました。標準正規分布とは平均0、分散1²である正規分布N(0,1²)のことをいいます。

標準正規分布の密度関数は下のようになります。

この図から分かるように標準正規分布において、k = 1.96 のとき、95%となります。標準正規分布では、その密度関数の-∞から1.96までの積分したものが0.95、つまり全体の 95% になることは分かりました。

次に標準正規分布を変形していって、母集団の分布にしていくことにします。

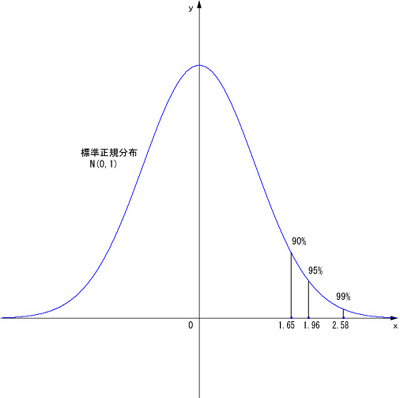
まず下の図のように標準正規分布（青の曲線）をy軸方向に1/σ倍します（赤の曲線）。

標準正規分布において-∞から k までの積分が全体に占める割合を X% とすると、赤い曲線の-∞から k までの積分が全体に占める割合も X% です。

y 軸方向に1/σ倍したら、次は x 軸方向にσ倍します。

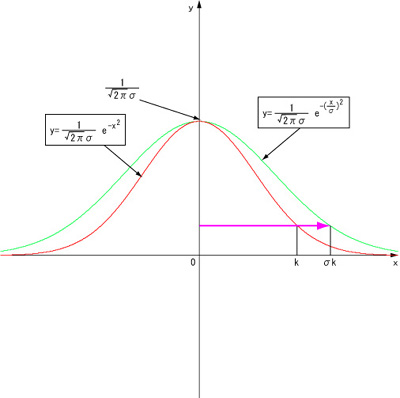
こうしてできた緑の曲線はN(0,σ²)の正規分布です。この密度関数は-∞から σk まで積分すると、全体の X% となります。

最後にこのN(0,σ²)を x 軸方向にμだけ平行移動すると、下の図のような正規分布N(μ,σ²)になるわけです。

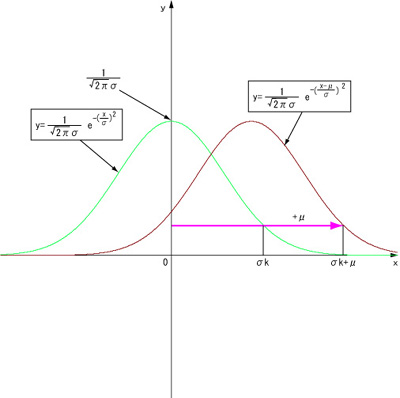
こうして、標準正規分布から、めでたく正規分布N(μ,σ²)に辿り着いたわけです。しかし単純にσk+μと統計量との比較してはいけないわけで、最初の例でいうと、このクラスが優れているかどうかは、そのクラスの人数を n 人とすると、その平均点は、母集団から無作為に選んだ n 人の平均点の分布と比較される必要があるわけです。

無限母集団がN(μ,σ²)の正規分布であるとき、その母集団から無作為に選んだ n 個の標本(x₁,x₂,x₃,…,x_n)の平均は、

u = ( x₁ + x₂ + x₃ + … + x_n )/n

であらわすことができます。

この平均の、平均と分散はそれぞれ、

E(u) = μ, V(u) = σ²/n

となります。ということは、n 個の標本平均を母平均と比較するときは、母集団を無作為に n 個ずつ抽出し、その平均の分布と比較しなければならないわけです。

つまり上のグラフでいうσk+μと比較するのではなくて、(σ/√n)・k+μと比較しなければならないのです。

クラスの平均点が x~ であったとすると、

x~ ＞ (σ/√n)・k+μ

が言えて初めて、クラスの平均が全国平均よりも優れていると言えるわけです。

実際にはこの式を変形して、

(x~ - μ)/(σ/√n)

が k ( 有意水準 α=0.05 なら 1.96 ) よりも大きければ母平均よりも標本平均の方が大きいと言えるわけです。（参照：母平均の検定）